Vectors and Parallel Data#
Vectors (denoted by Vec) are used to store discrete PDE solutions, right-hand sides for
linear systems, etc. Users can create and manipulate entries in vectors directly with a basic, low-level interface or
they can use the PETSc DM objects to connect actions on vectors to the type of discretization and grid that they are
working with. These higher-level interfaces handle much of the details of the interactions with vectors and hence, are preferred
in most situations. This chapter is organized as follows:
Setting vector values
Creating Vectors#
PETSc provides many ways to create vectors. The most basic, where the user is responsible for managing the
parallel distribution of the vector entries, and a variety of higher-level approaches, based on DM, for classes of problems such
as structured grids, staggered grids, unstructured grids, networks, and particles.
The most basic way to create a vector with a local size of m and a global size of M, is to
use
VecCreate(MPI_Comm comm,Vec *v);
VecSetSizes(Vec v, PetscInt m, PetscInt M);
VecSetFromOptions(Vec v);
which automatically generates the appropriate vector type (sequential or
parallel) over all processes in comm. The option -vec_type <type>
can be used in conjunction with
VecSetFromOptions() to specify the use of a particular type of vector. For example, for NVIDIA GPU CUDA, use cuda.
The GPU-based vectors allow
one to set values on either the CPU or GPU but do their computations on the GPU.
We emphasize that all processes in comm must call the vector
creation routines since these routines are collective on all
processes in the communicator. If you are unfamiliar with MPI
communicators, see the discussion in Writing PETSc Programs. In addition, if a sequence of creation routines is
used, they must be called in the same order for each process in the
communicator.
Instead of, or before calling VecSetFromOptions(), one can call
One can create vectors whose entries are stored on GPUs using the convenience routine,
VecCreateMPICUDA(MPI_Comm comm,PetscInt m,PetscInt M,Vec *x);
There are convenience creation routines for almost all vector types; we recommend using the more verbose form because it allows selecting CPU or GPU simulations at runtime.
For applications running in parallel that involve multi-dimensional structured grids, unstructured grids, networks, etc, it is cumbersome
for users to explicitly manage the needed local and global sizes of the vectors. Hence, PETSc provides a powerful abstract
object called the DM to help manage the vectors and matrices needed for such applications. Parallel vectors can be created easily with
DMCreateGlobalVector(DM dm,Vec *v)
The DM object, see DMDA - Creating vectors for structured grids, DMSTAG - Creating vectors for staggered grids, and DMPlex: Unstructured Grids for more details on DM for structured grids, staggered
structured grids, and for unstructured grids,
manages creating the correctly sized parallel vectors efficiently. One controls the type of vector that DM creates by calling
DMSetVecType(DM dm,VecType vt)
or by calling DMSetFromOptions(DM dm) and using the option -dm_vec_type <standard or cuda or kokkos etc>
DMDA - Creating vectors for structured grids#
Each DM type is suitable for a family of problems. The first of these, DMDA
are intended for use with logically structured rectangular grids
when communication of nonlocal data is needed before certain local
computations can occur. DMDA is designed only for
the case in which data can be thought of as being stored in a standard
multidimensional array; thus, DMDA are not intended for
parallelizing unstructured grid problems, etc.
For example, a typical situation one encounters in solving PDEs in
parallel is that, to evaluate a local function, f(x), each process
requires its local portion of the vector x as well as its ghost
points (the bordering portions of the vector that are owned by
neighboring processes). Figure Ghost Points for Two Stencil Types on the Seventh Process illustrates the
ghost points for the seventh process of a two-dimensional, structured
parallel grid. Each box represents a process; the ghost points for the
seventh process’s local part of a parallel array are shown in gray.
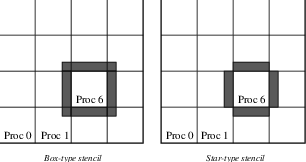
Fig. 3 Ghost Points for Two Stencil Types on the Seventh Process#
The DMDA object
contains parallel data layout information and communication
information and is used to create vectors and matrices with
the proper layout.
One creates a DMDA two
dimensions with the convenience routine
DMDACreate2d(MPI_Comm comm,DMBoundaryType xperiod,DMBoundaryType yperiod,DMDAStencilType st,PetscInt M, PetscInt N,PetscInt m,PetscInt n,PetscInt dof,PetscInt s,PetscInt *lx,PetscInt *ly,DM *da);
The arguments M and N indicate the global numbers of grid points
in each direction, while m and n denote the process partition in
each direction; m*n must equal the number of processes in the MPI
communicator, comm. Instead of specifying the process layout, one
may use PETSC_DECIDE for m and n so that PETSc will
select the partition. The type of periodicity of the array
is specified by xperiod and yperiod, which can be
DM_BOUNDARY_NONE (no periodicity), DM_BOUNDARY_PERIODIC
(periodic in that direction), DM_BOUNDARY_TWIST (periodic in that
direction, but identified in reverse order), DM_BOUNDARY_GHOSTED ,
or DM_BOUNDARY_MIRROR. The argument dof indicates the number of
degrees of freedom at each array point, and s is the stencil width
(i.e., the width of the ghost point region). The optional arrays lx
and ly may contain the number of nodes along the x and y axis for
each cell, i.e. the dimension of lx is m and the dimension of
ly is n; alternately, NULL may be passed in.
Two types of DMDA communication data structures can be
created, as specified by st. Star-type stencils that radiate outward
only in the coordinate directions are indicated by
DMDA_STENCIL_STAR, while box-type stencils are specified by
DMDA_STENCIL_BOX. For example, for the two-dimensional case,
DMDA_STENCIL_STAR with width 1 corresponds to the standard 5-point
stencil, while DMDA_STENCIL_BOX with width 1 denotes the standard
9-point stencil. In both instances, the ghost points are identical, the
only difference being that with star-type stencils, certain ghost points
are ignored, substantially decreasing the number of messages sent. Note
that the DMDA_STENCIL_STAR stencils can save interprocess
communication in two and three dimensions.
These DMDA stencils have nothing directly to do with a specific finite
difference stencil one might choose to use for discretization; they
only ensure that the correct values are in place for the application of a
user-defined finite difference stencil (or any other discretization
technique).
The commands for creating DMDA
in one and three dimensions are analogous:
DMDACreate1d(MPI_Comm comm,DMBoundaryType xperiod,PetscInt M,PetscInt w,PetscInt s,PetscInt *lc,DM *inra);
DMDACreate3d(MPI_Comm comm,DMBoundaryType xperiod,DMBoundaryType yperiod,DMBoundaryType zperiod, DMDAStencilType stencil_type,PetscInt M,PetscInt N,PetscInt P,PetscInt m,PetscInt n,PetscInt p,PetscInt w,PetscInt s,PetscInt *lx,PetscInt *ly,PetscInt *lz,DM *inra);
The routines to create a DM are collective so that all
processes in the communicator comm must call the same creation routines in the same order.
A DM may be created, and its type set with
Then DMType specific operations can be performed to provide information from which the specifics of the
DM will be provided. For example,
DMSetDimension(dm, 1);
DMDASetSizes(dm, M, 1, 1));
DMDASetDof(dm, 1));
DMSetUp(dm);
We now very briefly introduce a few more DMType.
DMSTAG - Creating vectors for staggered grids#
For structured grids with staggered data (living on elements, faces, edges,
and/or vertices), the DMSTAG object is available. It behaves much
like DMDA.
See DMSTAG: Staggered, Structured Grid for discussion of creating vectors with DMSTAG.
DMPLEX - Creating vectors for unstructured grids#
See DMPlex: Unstructured Grids for a discussion of creating vectors with DMPLEX.
DMNETWORK - Creating vectors for networks#
See Networks for discussion of creating vectors with DMNETWORK.
Common vector functions and operations#
One can examine (print out) a vector with the command
VecView(Vec x,PetscViewer v);
To print the vector to the screen, one can use the viewer
PETSC_VIEWER_STDOUT_WORLD, which ensures that parallel vectors are
printed correctly to stdout. To display the vector in an X-window,
one can use the default X-windows viewer PETSC_VIEWER_DRAW_WORLD, or
one can create a viewer with the routine PetscViewerDrawOpen(). A
variety of viewers are discussed further in
Viewers: Looking at PETSc Objects.
To create a new vector of the same format and parallel layout as an existing vector, use
VecDuplicate(Vec old,Vec *new);
To create several new vectors of the same format as an existing vector, use
VecDuplicateVecs(Vec old,PetscInt n,Vec **new);
This routine creates an array of pointers to vectors. The two routines
are useful because they allow one to write library code that does
not depend on the particular format of the vectors being used. Instead,
the subroutines can automatically create work vectors based on
the specified existing vector. As discussed in
Duplicating Multiple Vectors, the Fortran interface for
VecDuplicateVecs() differs slightly.
When a vector is no longer needed, it should be destroyed with the command
VecDestroy(Vec *x);
To destroy an array of vectors, use the command
VecDestroyVecs(PetscInt n,Vec **vecs);
Note that the Fortran interface for VecDestroyVecs() differs
slightly, as described in Duplicating Multiple Vectors.
It is also possible to create vectors that use an array the user provides rather than having PETSc internally allocate the array space. Such vectors can be created with the routines such as
VecCreateSeqWithArray(PETSC_COMM_SELF,PetscInt bs,PetscInt n,PetscScalar *array,Vec *V);
VecCreateMPIWithArray(MPI_Comm comm,PetscInt bs,PetscInt n,PetscInt N,PetscScalar *array,Vec *V);
VecCreateMPICUDAWithArray(MPI_Comm comm,PetscInt bs,PetscInt n,PetscInt N,PetscScalar *array,Vec *V);
The array pointer should be a GPU memory location for GPU vectors.
Note that here, one must provide the value n; it cannot be
PETSC_DECIDE and the user is responsible for providing enough space
in the array; n*sizeof(PetscScalar).
Assembling (putting values in) vectors#
One can assign a single value to all components of a vector with
VecSet(Vec x,PetscScalar value);
Assigning values to individual vector components is more complicated to make it possible to write efficient parallel code. Assigning a set of components on a CPU is a two-step process: one first calls
VecSetValues(Vec x,PetscInt n,PetscInt *indices,PetscScalar *values,INSERT_VALUES);
any number of times on any or all of the processes. The argument n
gives the number of components being set in this insertion. The integer
array indices contains the global component indices, and
values is the array of values to be inserted at those global component index locations. Any process can set
any vector components; PETSc ensures that they are automatically
stored in the correct location. Once all of the values have been
inserted with VecSetValues(), one must call
VecAssemblyBegin(Vec x);
followed by
VecAssemblyEnd(Vec x);
to perform any needed message passing of nonlocal components. In order to allow the overlap of communication and calculation, the user’s code can perform any series of other actions between these two calls while the messages are in transition.
Example usage of VecSetValues() may be found in src/vec/vec/tutorials/ex2.c
or src/vec/vec/tutorials/ex2f.F90.
Rather than inserting elements in a vector, one may wish to add values. This process is also done with the command
VecSetValues(Vec x,PetscInt n,PetscInt *indices, PetscScalar *values,ADD_VALUES);
Again, one must call the assembly routines VecAssemblyBegin() and
VecAssemblyEnd() after all of the values have been added. Note that
addition and insertion calls to VecSetValues() cannot be mixed.
Instead, one must add and insert vector elements in phases, with
intervening calls to the assembly routines. This phased assembly
procedure overcomes the nondeterministic behavior that would occur if
two different processes generated values for the same location, with one
process adding while the other is inserting its value. (In this case, the
addition and insertion actions could be performed in either order, thus
resulting in different values at the particular location. Since PETSc
does not allow the simultaneous use of INSERT_VALUES and
ADD_VALUES this nondeterministic behavior will not occur in PETSc.)
You can call VecGetValues() to pull local values from a vector (but
not off-process values).
For vectors obtained with DMCreateGlobalVector(), on can use VecSetValuesLocal() to set values into
a global vector but using the local (ghosted) vector indexing of the vector entries. See also Local to global mappings
that allows one to provide arbitrary local-to-global mapping when not working with a DM.
It is also possible to interact directly with the arrays that the vector values are stored
in. The routine VecGetArray() returns a pointer to the elements local to
the process:
VecGetArray(Vec v,PetscScalar **array);
When access to the array is no longer needed, the user should call
VecRestoreArray(Vec v, PetscScalar **array);
If the values do not need to be modified, the routines
VecGetArrayRead(Vec v, const PetscScalar **array);
VecRestoreArrayRead(Vec v, const PetscScalar **array);
should be used instead.
Listing: SNES Tutorial src/snes/tutorials/ex1.c
PetscErrorCode FormFunction1(SNES snes, Vec x, Vec f, void *ctx)
{
const PetscScalar *xx;
PetscScalar *ff;
PetscFunctionBeginUser;
/*
Get pointers to vector data.
- For default PETSc vectors, VecGetArray() returns a pointer to
the data array. Otherwise, the routine is implementation dependent.
- You MUST call VecRestoreArray() when you no longer need access to
the array.
*/
PetscCall(VecGetArrayRead(x, &xx));
PetscCall(VecGetArray(f, &ff));
/* Compute function */
ff[0] = xx[0] * xx[0] + xx[0] * xx[1] - 3.0;
ff[1] = xx[0] * xx[1] + xx[1] * xx[1] - 6.0;
/* Restore vectors */
PetscCall(VecRestoreArrayRead(x, &xx));
PetscCall(VecRestoreArray(f, &ff));
PetscFunctionReturn(PETSC_SUCCESS);
Minor differences exist in the Fortran interface for VecGetArray()
and VecRestoreArray(), as discussed in
Routines that Return Fortran Allocatable Arrays. It is important to note that
VecGetArray() and VecRestoreArray() do not copy the vector
elements; they merely give users direct access to the vector elements.
Thus, these routines require essentially no time to call and can be used
efficiently.
For GPU vectors, one can access either the values on the CPU as described above or one can call, for example,
VecCUDAGetArray(Vec v, PetscScalar **array);
Listing: SNES Tutorial src/snes/tutorials/ex47cu.cu
PetscCall(VecCUDAGetArrayRead(xlocal, &xarray));
PetscCall(VecCUDAGetArrayWrite(f, &farray));
if (rank) xstartshift = 1;
else xstartshift = 0;
if (rank != size - 1) xendshift = 1;
else xendshift = 0;
PetscCall(VecGetOwnershipRange(f, &fstart, NULL));
PetscCall(VecGetLocalSize(x, &lsize));
// clang-format off
try {
thrust::for_each(
thrust::make_zip_iterator(
thrust::make_tuple(
thrust::device_ptr<PetscScalar>(farray),
thrust::device_ptr<const PetscScalar>(xarray + xstartshift),
thrust::device_ptr<const PetscScalar>(xarray + xstartshift + 1),
thrust::device_ptr<const PetscScalar>(xarray + xstartshift - 1),
thrust::counting_iterator<int>(fstart),
thrust::constant_iterator<int>(Mx),
thrust::constant_iterator<PetscScalar>(hx))),
thrust::make_zip_iterator(
thrust::make_tuple(
thrust::device_ptr<PetscScalar>(farray + lsize),
thrust::device_ptr<const PetscScalar>(xarray + lsize - xendshift),
thrust::device_ptr<const PetscScalar>(xarray + lsize - xendshift + 1),
thrust::device_ptr<const PetscScalar>(xarray + lsize - xendshift - 1),
thrust::counting_iterator<int>(fstart) + lsize,
thrust::constant_iterator<int>(Mx),
thrust::constant_iterator<PetscScalar>(hx))),
ApplyStencil());
}
or
VecGetArrayAndMemType(Vec v, PetscScalar **array,PetscMemType *mtype);
which, in the first case, returns a GPU memory address and, in the second case, returns either a CPU or GPU memory
address depending on the type of the vector. One can then launch a GPU kernel function that accesses the
vector’s memory for usage with GPUs. When computing on GPUs, VecSetValues() is not used! One always accesses the vector’s arrays and passes them
to the GPU code.
It can also be convenient to treat the vector entries as a Kokkos view. One first creates Kokkos vectors and then calls
VecGetKokkosView(Vec v, Kokkos::View<const PetscScalar*,MemorySpace> *kv)
to set or access the vector entries.
Of course, to provide the correct values to a vector, one must know what parts of the vector are owned by each MPI process. For parallel vectors, either CPU or GPU-based, it is possible to determine a process’s local range with the routine
VecGetOwnershipRange(Vec vec,PetscInt *start,PetscInt *end);
The argument start indicates the first component owned by the local
process, while end specifies one more than the last owned by the
local process. This command is useful, for instance, in assembling
parallel vectors.
The number of elements stored locally can be accessed with
VecGetLocalSize(Vec v,PetscInt *size);
The global vector length can be determined by
VecGetSize(Vec v,PetscInt *size);
DMDA - Setting vector values#
PETSc provides an easy way to set values into the DMDA vectors and
access them using the natural grid indexing. This is done with the
routines
DMDAVecGetArray(DM da,Vec l,void *array);
... use the array indexing it with 1, 2, or 3 dimensions ...
... depending on the dimension of the DMDA ...
DMDAVecRestoreArray(DM da,Vec l,void *array);
DMDAVecGetArrayRead(DM da,Vec l,void *array);
... use the array indexing it with 1, 2, or 3 dimensions ...
... depending on the dimension of the DMDA ...
DMDAVecRestoreArrayRead(DM da,Vec l,void *array);
where array is a multidimensional C array with the same dimension as da, and
DMDAVecGetArrayDOF(DM da,Vec l,void *array);
... use the array indexing it with 2, 3, or 4 dimensions ...
... depending on the dimension of the DMDA ...
DMDAVecRestoreArrayDOF(DM da,Vec l,void *array);
DMDAVecGetArrayDOFRead(DM da,Vec l,void *array);
... use the array indexing it with 2, 3, or 4 dimensions ...
... depending on the dimension of the DMDA ...
DMDAVecRestoreArrayDOFRead(DM da,Vec l,void *array);
where array is a multidimensional C array with one more dimension than
da. The vector l can be either a global vector or a local
vector. The array is accessed using the usual global indexing on
the entire grid, but the user may only refer to this array’s local and ghost
entries as all other entries are undefined. For example,
for a scalar problem in two dimensions, one could use
PetscScalar **f,**u;
...
DMDAVecGetArrayRead(DM da,Vec local,&u);
DMDAVecGetArray(DM da,Vec global,&f);
...
f[i][j] = u[i][j] - ...
...
DMDAVecRestoreArrayRead(DM da,Vec local,&u);
DMDAVecRestoreArray(DM da,Vec global,&f);
Listing: SNES Tutorial src/snes/tutorials/ex3.c
PetscErrorCode FormFunction(SNES snes, Vec x, Vec f, void *ctx)
{
ApplicationCtx *user = (ApplicationCtx *)ctx;
DM da = user->da;
PetscScalar *ff, d;
const PetscScalar *xx, *FF;
PetscInt i, M, xs, xm;
Vec xlocal;
PetscFunctionBeginUser;
PetscCall(DMGetLocalVector(da, &xlocal));
/*
Scatter ghost points to local vector, using the 2-step process
DMGlobalToLocalBegin(), DMGlobalToLocalEnd().
By placing code between these two statements, computations can
be done while messages are in transition.
*/
PetscCall(DMGlobalToLocalBegin(da, x, INSERT_VALUES, xlocal));
PetscCall(DMGlobalToLocalEnd(da, x, INSERT_VALUES, xlocal));
/*
Get pointers to vector data.
- The vector xlocal includes ghost point; the vectors x and f do
NOT include ghost points.
- Using DMDAVecGetArray() allows accessing the values using global ordering
*/
PetscCall(DMDAVecGetArrayRead(da, xlocal, (void *)&xx));
PetscCall(DMDAVecGetArray(da, f, &ff));
PetscCall(DMDAVecGetArrayRead(da, user->F, (void *)&FF));
/*
Get local grid boundaries (for 1-dimensional DMDA):
xs, xm - starting grid index, width of local grid (no ghost points)
*/
PetscCall(DMDAGetCorners(da, &xs, NULL, NULL, &xm, NULL, NULL));
PetscCall(DMDAGetInfo(da, NULL, &M, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL));
/*
Set function values for boundary points; define local interior grid point range:
xsi - starting interior grid index
xei - ending interior grid index
*/
if (xs == 0) { /* left boundary */
ff[0] = xx[0];
xs++;
xm--;
}
if (xs + xm == M) { /* right boundary */
ff[xs + xm - 1] = xx[xs + xm - 1] - 1.0;
xm--;
}
/*
Compute function over locally owned part of the grid (interior points only)
*/
d = 1.0 / (user->h * user->h);
for (i = xs; i < xs + xm; i++) ff[i] = d * (xx[i - 1] - 2.0 * xx[i] + xx[i + 1]) + xx[i] * xx[i] - FF[i];
/*
Restore vectors
*/
PetscCall(DMDAVecRestoreArrayRead(da, xlocal, (void *)&xx));
PetscCall(DMDAVecRestoreArray(da, f, &ff));
PetscCall(DMDAVecRestoreArrayRead(da, user->F, (void *)&FF));
PetscCall(DMRestoreLocalVector(da, &xlocal));
PetscFunctionReturn(PETSC_SUCCESS);
The recommended approach for multi-component PDEs is to declare a
struct representing the fields defined at each node of the grid,
e.g.
typedef struct {
PetscScalar u,v,omega,temperature;
} Node;
and write the residual evaluation using
Node **f,**u;
DMDAVecGetArray(DM da,Vec local,&u);
DMDAVecGetArray(DM da,Vec global,&f);
...
f[i][j].omega = ...
...
DMDAVecRestoreArray(DM da,Vec local,&u);
DMDAVecRestoreArray(DM da,Vec global,&f);
The DMDAVecGetArray routines are also provided for GPU access with CUDA, HIP, and Kokkos. For example,
DMDAVecGetKokkosOffsetView(DM da,Vec vec,Kokkos::View<const PetscScalar*XX*,MemorySpace> *ov)
where *XX* can contain any number of *. This allows one to write very natural Kokkos multi-dimensional parallel for kernels
that act on the local portion of DMDA vectors.
Listing: SNES Tutorial src/snes/tutorials/ex3k.kokkos.cxx
PetscErrorCode KokkosFunction(SNES snes, Vec x, Vec r, void *ctx)
{
ApplicationCtx *user = (ApplicationCtx *)ctx;
DM da = user->da;
PetscScalar d;
PetscInt M;
Vec xl;
PetscScalarKokkosOffsetView R;
ConstPetscScalarKokkosOffsetView X, F;
PetscFunctionBeginUser;
PetscCall(DMGetLocalVector(da, &xl));
PetscCall(DMGlobalToLocal(da, x, INSERT_VALUES, xl));
d = 1.0 / (user->h * user->h);
PetscCall(DMDAGetInfo(da, NULL, &M, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL));
PetscCall(DMDAVecGetKokkosOffsetView(da, xl, &X)); /* read only */
PetscCall(DMDAVecGetKokkosOffsetViewWrite(da, r, &R)); /* write only */
PetscCall(DMDAVecGetKokkosOffsetView(da, user->F, &F)); /* read only */
Kokkos::parallel_for(
Kokkos::RangePolicy<>(R.begin(0), R.end(0)), KOKKOS_LAMBDA(int i) {
if (i == 0) R(0) = X(0); /* left boundary */
else if (i == M - 1) R(i) = X(i) - 1.0; /* right boundary */
else R(i) = d * (X(i - 1) - 2.0 * X(i) + X(i + 1)) + X(i) * X(i) - F(i); /* interior */
});
PetscCall(DMDAVecRestoreKokkosOffsetView(da, xl, &X));
PetscCall(DMDAVecRestoreKokkosOffsetViewWrite(da, r, &R));
PetscCall(DMDAVecRestoreKokkosOffsetView(da, user->F, &F));
PetscCall(DMRestoreLocalVector(da, &xl));
PetscFunctionReturn(PETSC_SUCCESS);
The global indices of the lower left corner of the local portion of vectors obtained from DMDA
as well as the local array size can be obtained with the commands
These values can then be used as loop bounds for local function evaluations as demonstrated in the function examples above.
The first version excludes ghost points, while the second
includes them. The routine DMDAGetGhostCorners() deals with the fact
that subarrays along boundaries of the problem domain have ghost points
only on their interior edges, but not on their boundary edges.
When either type of stencil is used, DMDA_STENCIL_STAR or
DMDA_STENCIL_BOX, the local vectors (with the ghost points)
represent rectangular arrays, including the extra corner elements in the
DMDA_STENCIL_STAR case. This configuration provides simple access to
the elements by employing two- (or three–) dimensional indexing. The
only difference between the two cases is that when DMDA_STENCIL_STAR
is used, the extra corner components are not scattered between the
processes and thus contain undefined values that should not be used.
DMSTAG - Setting vector values#
For structured grids with staggered data (living on elements, faces, edges,
and/or vertices), the DMStag object is available. It behaves
like DMDA; see the DMSTAG manual page for more information.
Listing: SNES Tutorial src/dm/impls/stag/tutorials/ex6.c
static PetscErrorCode UpdateVelocity_2d(const Ctx *ctx, Vec velocity, Vec stress, Vec buoyancy)
{
Vec velocity_local, stress_local, buoyancy_local;
PetscInt ex, ey, startx, starty, nx, ny;
PetscInt slot_coord_next, slot_coord_element, slot_coord_prev;
PetscInt slot_vx_left, slot_vy_down, slot_buoyancy_down, slot_buoyancy_left;
PetscInt slot_txx, slot_tyy, slot_txy_downleft, slot_txy_downright, slot_txy_upleft;
const PetscScalar **arr_coord_x, **arr_coord_y;
const PetscScalar ***arr_stress, ***arr_buoyancy;
PetscScalar ***arr_velocity;
PetscFunctionBeginUser;
/* Prepare direct access to buoyancy data */
PetscCall(DMStagGetLocationSlot(ctx->dm_buoyancy, DMSTAG_LEFT, 0, &slot_buoyancy_left));
PetscCall(DMStagGetLocationSlot(ctx->dm_buoyancy, DMSTAG_DOWN, 0, &slot_buoyancy_down));
PetscCall(DMGetLocalVector(ctx->dm_buoyancy, &buoyancy_local));
PetscCall(DMGlobalToLocal(ctx->dm_buoyancy, buoyancy, INSERT_VALUES, buoyancy_local));
PetscCall(DMStagVecGetArrayRead(ctx->dm_buoyancy, buoyancy_local, (void *)&arr_buoyancy));
/* Prepare read-only access to stress data */
PetscCall(DMStagGetLocationSlot(ctx->dm_stress, DMSTAG_ELEMENT, 0, &slot_txx));
PetscCall(DMStagGetLocationSlot(ctx->dm_stress, DMSTAG_ELEMENT, 1, &slot_tyy));
PetscCall(DMStagGetLocationSlot(ctx->dm_stress, DMSTAG_UP_LEFT, 0, &slot_txy_upleft));
PetscCall(DMStagGetLocationSlot(ctx->dm_stress, DMSTAG_DOWN_LEFT, 0, &slot_txy_downleft));
PetscCall(DMStagGetLocationSlot(ctx->dm_stress, DMSTAG_DOWN_RIGHT, 0, &slot_txy_downright));
PetscCall(DMGetLocalVector(ctx->dm_stress, &stress_local));
PetscCall(DMGlobalToLocal(ctx->dm_stress, stress, INSERT_VALUES, stress_local));
PetscCall(DMStagVecGetArrayRead(ctx->dm_stress, stress_local, (void *)&arr_stress));
/* Prepare read-write access to velocity data */
PetscCall(DMStagGetLocationSlot(ctx->dm_velocity, DMSTAG_LEFT, 0, &slot_vx_left));
PetscCall(DMStagGetLocationSlot(ctx->dm_velocity, DMSTAG_DOWN, 0, &slot_vy_down));
PetscCall(DMGetLocalVector(ctx->dm_velocity, &velocity_local));
PetscCall(DMGlobalToLocal(ctx->dm_velocity, velocity, INSERT_VALUES, velocity_local));
PetscCall(DMStagVecGetArray(ctx->dm_velocity, velocity_local, &arr_velocity));
/* Prepare read-only access to coordinate data */
PetscCall(DMStagGetProductCoordinateLocationSlot(ctx->dm_velocity, DMSTAG_LEFT, &slot_coord_prev));
PetscCall(DMStagGetProductCoordinateLocationSlot(ctx->dm_velocity, DMSTAG_RIGHT, &slot_coord_next));
PetscCall(DMStagGetProductCoordinateLocationSlot(ctx->dm_velocity, DMSTAG_ELEMENT, &slot_coord_element));
PetscCall(DMStagGetProductCoordinateArrays(ctx->dm_velocity, (void *)&arr_coord_x, (void *)&arr_coord_y, NULL));
/* Iterate over interior of the domain, updating the velocities */
PetscCall(DMStagGetCorners(ctx->dm_velocity, &startx, &starty, NULL, &nx, &ny, NULL, NULL, NULL, NULL));
for (ey = starty; ey < starty + ny; ++ey) {
for (ex = startx; ex < startx + nx; ++ex) {
/* Update y-velocity */
if (ey > 0) {
const PetscScalar dx = arr_coord_x[ex][slot_coord_next] - arr_coord_x[ex][slot_coord_prev];
const PetscScalar dy = arr_coord_y[ey][slot_coord_element] - arr_coord_y[ey - 1][slot_coord_element];
const PetscScalar B = arr_buoyancy[ey][ex][slot_buoyancy_down];
arr_velocity[ey][ex][slot_vy_down] += B * ctx->dt * ((arr_stress[ey][ex][slot_txy_downright] - arr_stress[ey][ex][slot_txy_downleft]) / dx + (arr_stress[ey][ex][slot_tyy] - arr_stress[ey - 1][ex][slot_tyy]) / dy);
}
/* Update x-velocity */
DMPLEX - Setting vector values#
See DMPlex: Unstructured Grids for a discussion on setting vector values with DMPLEX.
DMNETWORK - Setting vector values#
See Networks for a discussion on setting vector values with DMNETWORK.
Basic Vector Operations#
Function Name |
Operation |
|---|---|
|
\(y = y + a*x\) |
|
\(y = x + a*y\) |
|
\(w = a*x + y\) |
|
\(y = a*x + b*y\) |
|
\(z = a*x + b*y + c*z\) |
|
\(x = a*x\) |
|
\(r = \bar{x}^T*y\) |
|
\(r = x'*y\) |
\(r = ||x||_{type}\) |
|
|
\(r = \sum x_{i}\) |
\(y = x\) |
|
\(y = x\) while \(x = y\) |
|
|
\(w_{i} = x_{i}*y_{i}\) |
|
\(w_{i} = x_{i}/y_{i}\) |
|
\(r[i] = \bar{x}^T*y[i]\) |
|
\(r[i] = x^T*y[i]\) |
|
\(y = y + \sum_i a_{i}*x[i]\) |
\(r = \max x_{i}\) |
|
\(r = \min x_{i}\) |
|
\(x_i = |x_{i}|\) |
|
|
\(x_i = 1/x_{i}\) |
|
\(x_i = s + x_{i}\) |
|
\(x_i = \alpha\) |
As the table lists, we have chosen certain
basic vector operations to support within the PETSc vector library.
These operations were selected because they often arise in application
codes. The NormType argument to VecNorm() is one of NORM_1,
NORM_2, or NORM_INFINITY. The 1-norm is \(\sum_i |x_{i}|\),
the 2-norm is \(( \sum_{i} x_{i}^{2})^{1/2}\) and the infinity norm
is \(\max_{i} |x_{i}|\).
In addition to VecDot() and VecMDot() and VecNorm(), PETSc
provides split phase versions of this functionality that allow several independent
inner products and/or norms to share the same communication (thus
improving parallel efficiency). For example, one may have code such as
This code works fine, but it performs four separate parallel communication operations. Instead, one can write
VecDotBegin(Vec x,Vec y,PetscScalar *dot);
VecMDotBegin(Vec x, PetscInt nv,Vec y[],PetscScalar *dot);
VecNormBegin(Vec x,NormType NORM_2,PetscReal *norm2);
VecNormBegin(Vec x,NormType NORM_1,PetscReal *norm1);
VecDotEnd(Vec x,Vec y,PetscScalar *dot);
VecMDotEnd(Vec x, PetscInt nv,Vec y[],PetscScalar *dot);
VecNormEnd(Vec x,NormType NORM_2,PetscReal *norm2);
VecNormEnd(Vec x,NormType NORM_1,PetscReal *norm1);
With this code, the communication is delayed until the first call to
VecxxxEnd() at which a single MPI reduction is used to communicate
all the values. It is required that the calls to the
VecxxxEnd() are performed in the same order as the calls to the
VecxxxBegin(); however, if you mistakenly make the calls in the
wrong order, PETSc will generate an error informing you of this. There
are additional routines VecTDotBegin() and VecTDotEnd(),
VecMTDotBegin(), VecMTDotEnd().
For GPU vectors (like CUDA), the numerical computations will, by default, run on the GPU. Any
scalar output, like the result of a VecDot() are placed in CPU memory.
Local/global vectors and communicating between vectors#
Many PDE problems require ghost (or halo) values in each MPI process or even more general parallel communication
of vector values. These values are needed
to perform function evaluation on that MPI process. The exact structure of the ghost values needed
depends on the type of grid being used. DM provides a uniform API for communicating the needed
values. We introduce the concept in detail for DMDA.
Each DM object defines the layout of two vectors: a distributed
global vector and a local vector that includes room for the appropriate
ghost points. The DM object provides information about the size
and layout of these vectors. The user can create
vector objects that use the DM layout information with the
routines
DMCreateGlobalVector(DM da,Vec *g);
DMCreateLocalVector(DM da,Vec *l);
These vectors will generally serve as the building blocks for local and
global PDE solutions, etc. If additional vectors with such layout
information are needed in a code, they can be obtained by duplicating
l or g via VecDuplicate() or VecDuplicateVecs().
We emphasize that a DM provides the information needed to
communicate the ghost value information between processes. In most
cases, several different vectors can share the same communication
information (or, in other words, can share a given DM). The design
of the DM object makes this easy, as each DM operation may
operate on vectors of the appropriate size, as obtained via
DMCreateLocalVector() and DMCreateGlobalVector() or as produced
by VecDuplicate().
At certain stages of many applications, there is a need to work on a local portion of the vector that includes the ghost points. This may be done by scattering a global vector into its local parts by using the two-stage commands
DMGlobalToLocalBegin(DM da,Vec g,InsertMode iora,Vec l);
DMGlobalToLocalEnd(DM da,Vec g,InsertMode iora,Vec l);
which allows the overlap of communication and computation. Since the
global and local vectors, given by g and l, respectively, must
be compatible with the DM, da, they should be
generated by DMCreateGlobalVector() and DMCreateLocalVector()
(or be duplicates of such a vector obtained via VecDuplicate()). The
InsertMode can be ADD_VALUES or INSERT_VALUES among other possible values.
One can scatter the local vectors into the distributed global vector with the command
DMLocalToGlobal(DM da,Vec l,InsertMode mode,Vec g);
or the commands
DMLocalToGlobalBegin(DM da,Vec l,InsertMode mode,Vec g);
/* (Computation to overlap with communication) */
DMLocalToGlobalEnd(DM da,Vec l,InsertMode mode,Vec g);
In general this is used with an InsertMode of ADD_VALUES,
because if one wishes to insert values into the global vector, they
should access the global vector directly and put in the values.
A third type of DM scatter is from a local vector
(including ghost points that contain irrelevant values) to a local
vector with correct ghost point values. This scatter may be done with
the commands
DMLocalToLocalBegin(DM da,Vec l1,InsertMode iora,Vec l2);
DMLocalToLocalEnd(DM da,Vec l1,InsertMode iora,Vec l2);
Since both local vectors, l1 and l2, must be compatible with da, they should be generated by
DMCreateLocalVector() (or be duplicates of such vectors obtained via
VecDuplicate()). The InsertMode can be either ADD_VALUES or
INSERT_VALUES.
In most applications, the local ghosted vectors are only needed temporarily during user “function evaluations”. PETSc provides an easy, light-weight (requiring essentially no CPU time) way to temporarily obtain these work vectors and return them when no longer needed. This is done with the routines
DMGetLocalVector(DM da,Vec *l);
... use the local vector l ...
DMRestoreLocalVector(DM da,Vec *l);
Low-level Vector Communication#
Most users of PETSc who can utilize a DM will not need to utilize the lower-level routines discussed in the rest of this section
and should skip ahead to Matrices.
To facilitate creating general vector scatters and gathers used, for example, in
updating ghost points for problems for which no DM currently exists
PETSc employs the concept of an index set, via the IS class. An
index set, a generalization of a set of integer indices, is
used to define scatters, gathers, and similar operations on vectors and
matrices. Much of the underlying code that implements DMGlobalToLocal communication is built
on the infrastructure discussed below.
The following command creates an index set based on a list of integers:
ISCreateGeneral(MPI_Comm comm,PetscInt n,PetscInt *indices,PetscCopyMode mode, IS *is);
When mode is PETSC_COPY_VALUES, this routine copies the n
indices passed to it by the integer array indices. Thus, the user
should be sure to free the integer array indices when it is no
longer needed, perhaps directly after the call to ISCreateGeneral().
The communicator, comm, should include all processes
using the IS.
Another standard index set is defined by a starting point (first)
and a stride (step), and can be created with the command
The meaning of n, first, and step correspond to the MATLAB notation
first:step:first+n*step.
Index sets can be destroyed with the command
On rare occasions, the user may need to access information directly from an index set. Several commands assist in this process:
ISGetSize(IS is,PetscInt *size);
ISStrideGetInfo(IS is,PetscInt *first,PetscInt *stride);
ISGetIndices(IS is,PetscInt **indices);
The function ISGetIndices() returns a pointer to a list of the
indices in the index set. For certain index sets, this may be a
temporary array of indices created specifically for the call.
Thus, once the user finishes using the array of indices, the routine
ISRestoreIndices(IS is, PetscInt **indices);
should be called to ensure that the system can free the space it may have used to generate the list of indices.
A blocked version of index sets can be created with the command
ISCreateBlock(MPI_Comm comm,PetscInt bs,PetscInt n,PetscInt *indices,PetscCopyMode mode, IS *is);
This version is used for defining operations in which each element of
the index set refers to a block of bs vector entries. Related
routines analogous to those described above exist as well, including
ISBlockGetIndices(), ISBlockGetSize(),
ISBlockGetLocalSize(), ISGetBlockSize().
Most PETSc applications use a particular DM object to manage the communication details needed for their grids.
In some rare cases, however, codes need to directly set up their required communication patterns. This is done using
PETSc’s VecScatter and PetscSF (for more general data than vectors). One
can select any subset of the components of a vector to insert or add to
any subset of the components of another vector. We refer to these
operations as generalized scatters, though they are a
combination of scatters and gathers.
To copy selected components from one vector to another, one uses the following set of commands:
VecScatterCreate(Vec x,IS ix,Vec y,IS iy,VecScatter *ctx);
VecScatterBegin(VecScatter ctx,Vec x,Vec y,INSERT_VALUES,SCATTER_FORWARD);
VecScatterEnd(VecScatter ctx,Vec x,Vec y,INSERT_VALUES,SCATTER_FORWARD);
VecScatterDestroy(VecScatter *ctx);
Here ix denotes the index set of the first vector, while iy
indicates the index set of the destination vector. The vectors can be
parallel or sequential. The only requirements are that the number of
entries in the index set of the first vector, ix, equals the number
in the destination index set, iy, and that the vectors be long
enough to contain all the indices referred to in the index sets. If both
x and y are parallel, their communicator must have the same set
of processes, but their process order can differ. The argument
INSERT_VALUES specifies that the vector elements will be inserted
into the specified locations of the destination vector, overwriting any
existing values. To add the components, rather than insert them, the
user should select the option ADD_VALUES instead of
INSERT_VALUES. One can also use MAX_VALUES or MIN_VALUES to
replace the destination with the maximal or minimal of its current value and
the scattered values.
To perform a conventional gather operation, the user makes the
destination index set, iy, be a stride index set with a stride of
one. Similarly, a conventional scatter can be done with an initial
(sending) index set consisting of a stride. The scatter routines are
collective operations (i.e. all processes that own a parallel vector
must call the scatter routines). When scattering from a parallel
vector to sequential vectors, each process has its own sequential vector
that receives values from locations as indicated in its own index set.
Similarly, in scattering from sequential vectors to a parallel vector,
each process has its own sequential vector that contributes to
the parallel vector.
Caution: When INSERT_VALUES is used, if two different processes
contribute different values to the same component in a parallel vector,
either value may be inserted. When ADD_VALUES is used, the
correct sum is added to the correct location.
In some cases, one may wish to “undo” a scatter, that is, perform the scatter backward, switching the roles of the sender and receiver. This is done by using
VecScatterBegin(VecScatter ctx,Vec y,Vec x,INSERT_VALUES,SCATTER_REVERSE);
VecScatterEnd(VecScatter ctx,Vec y,Vec x,INSERT_VALUES,SCATTER_REVERSE);
Note that the roles of the first two arguments to these routines must be
swapped whenever the SCATTER_REVERSE option is used.
Once a VecScatter object has been created, it may be used with any
vectors that have the same parallel data layout. That is, one can
call VecScatterBegin() and VecScatterEnd() with different
vectors than used in the call to VecScatterCreate() as long as they
have the same parallel layout (the number of elements on each process are
the same). Usually, these “different” vectors would have been obtained
via calls to VecDuplicate() from the original vectors used in the
call to VecScatterCreate().
VecGetValues() can only access
local values from the vector. To get off-process values, the user should
create a new vector where the components will be stored and then
perform the appropriate vector scatter. For example, if one desires to
obtain the values of the 100th and 200th entries of a parallel vector,
p, one could use a code such as that below. In this example, the
values of the 100th and 200th components are placed in the array values.
In this example, each process now has the 100th and 200th component, but
obviously, each process could gather any elements it needed, or none by
creating an index set with no entries.
Vec p, x; /* initial vector, destination vector */
VecScatter scatter; /* scatter context */
IS from, to; /* index sets that define the scatter */
PetscScalar *values;
PetscInt idx_from[] = {100,200}, idx_to[] = {0,1};
VecCreateSeq(PETSC_COMM_SELF,2,&x);
ISCreateGeneral(PETSC_COMM_SELF,2,idx_from,PETSC_COPY_VALUES,&from);
ISCreateGeneral(PETSC_COMM_SELF,2,idx_to,PETSC_COPY_VALUES,&to);
VecScatterCreate(p,from,x,to,&scatter);
VecScatterBegin(scatter,p,x,INSERT_VALUES,SCATTER_FORWARD);
VecScatterEnd(scatter,p,x,INSERT_VALUES,SCATTER_FORWARD);
VecGetArray(x,&values);
ISDestroy(&from);
ISDestroy(&to);
VecScatterDestroy(&scatter);
The scatter comprises two stages to allow for the overlap of
communication and computation. The introduction of the VecScatter
context allows the communication patterns for the scatter to be computed
once and reused repeatedly. Generally, even setting up the
communication for a scatter requires communication; hence, it is best to
reuse such information when possible.
Scatters provide a very general method for managing the communication of required ghost values for unstructured grid computations. One scatters the global vector into a local “ghosted” work vector, performs the computation on the local work vectors, and then scatters back into the global solution vector. In the simplest case, this may be written as
VecScatterBegin(VecScatter scatter,Vec globalin,Vec localin,InsertMode INSERT_VALUES, ScatterMode SCATTER_FORWARD);
VecScatterEnd(VecScatter scatter,Vec globalin,Vec localin,InsertMode INSERT_VALUES,ScatterMode SCATTER_FORWARD);
/* For example, do local calculations from localin to localout */
...
VecScatterBegin(VecScatter scatter,Vec localout,Vec globalout,InsertMode ADD_VALUES,ScatterMode SCATTER_REVERSE);
VecScatterEnd(VecScatter scatter,Vec localout,Vec globalout,InsertMode ADD_VALUES,ScatterMode SCATTER_REVERSE);
In this case, the scatter is used in a way similar to the usage of DMGlobalToLocal() and DMLocalToGlobal() discussed above.
Local to global mappings#
When working with a global representation of a vector
(usually on a vector obtained with DMCreateGlobalVector()) and a local
representation of the same vector that includes ghost points required
for local computation (obtained with DMCreateLocalVector()). PETSc provides routines to help map indices from
a local numbering scheme to the PETSc global numbering scheme, recall their use above for the routine VecSetValuesLocal() introduced above.
This is done via the following routines
ISLocalToGlobalMappingCreate(MPI_Comm comm,PetscInt bs,PetscInt N,PetscInt* globalnum,PetscCopyMode mode,ISLocalToGlobalMapping* ctx);
ISLocalToGlobalMappingApply(ISLocalToGlobalMapping ctx,PetscInt n,PetscInt *in,PetscInt *out);
ISLocalToGlobalMappingApplyIS(ISLocalToGlobalMapping ctx,IS isin,IS* isout);
ISLocalToGlobalMappingDestroy(ISLocalToGlobalMapping *ctx);
Here N denotes the number of local indices, globalnum contains
the global number of each local number, and ISLocalToGlobalMapping
is the resulting PETSc object that contains the information needed to
apply the mapping with either ISLocalToGlobalMappingApply() or
ISLocalToGlobalMappingApplyIS().
Note that the ISLocalToGlobalMapping routines serve a different
purpose than the AO routines. In the former case, they provide a
mapping from a local numbering scheme (including ghost points) to a
global numbering scheme, while in the latter, they provide a mapping
between two global numbering schemes. Many applications may use
both AO and ISLocalToGlobalMapping routines. The AO routines
are first used to map from an application global ordering (that has no
relationship to parallel processing, etc.) to the PETSc ordering scheme
(where each process has a contiguous set of indices in the numbering).
Then, to perform function or Jacobian evaluations locally on
each process, one works with a local numbering scheme that includes
ghost points. The mapping from this local numbering scheme back to the
global PETSc numbering can be handled with the
ISLocalToGlobalMapping routines.
If one is given a list of block indices in a global numbering, the routine
ISGlobalToLocalMappingApplyBlock(ISLocalToGlobalMapping ctx,ISGlobalToLocalMappingMode type,PetscInt nin,PetscInt idxin[],PetscInt *nout,PetscInt idxout[]);
will provide a new list of indices in the local numbering. Again,
negative values in idxin are left unmapped. But in addition, if
type is set to IS_GTOLM_MASK , then nout is set to nin
and all global values in idxin that are not represented in the local
to global mapping are replaced by -1. When type is set to
IS_GTOLM_DROP, the values in idxin that are not represented
locally in the mapping are not included in idxout, so that
potentially nout is smaller than nin. One must pass in an array
long enough to hold all the indices. One can call
ISGlobalToLocalMappingApplyBlock() with idxout equal to NULL
to determine the required length (returned in nout) and then
allocate the required space and call
ISGlobalToLocalMappingApplyBlock() a second time to set the values.
Often it is convenient to set elements into a vector using the local node numbering rather than the global node numbering (e.g., each process may maintain its own sublist of vertices and elements and number them locally). To set values into a vector with the local numbering, one must first call
and then call
VecSetValuesLocal(Vec x,PetscInt n,const PetscInt indices[],const PetscScalar values[],INSERT_VALUES);
Now the indices use the local numbering rather than the global,
meaning the entries lie in \([0,n)\) where \(n\) is the local
size of the vector. Global vectors obtained from a DM already have the global to local mapping
provided by the DM.
One can use global indices
with MatSetValues() or MatSetValuesStencil() to assemble global stiffness matrices. Alternately, the
global node number of each local node, including the ghost nodes, can be
obtained by calling
followed by
VecSetLocalToGlobalMapping(Vec v,ISLocalToGlobalMapping map);
MatSetLocalToGlobalMapping(Mat A,ISLocalToGlobalMapping rmapping,ISLocalToGlobalMapping cmapping);
Now, entries may be added to the vector and matrix using the local
numbering and VecSetValuesLocal() and MatSetValuesLocal().
The example
SNES Tutorial ex5
illustrates the use of a DMDA in the solution of a
nonlinear problem. The analogous Fortran program is
SNES Tutorial ex5f90;
see SNES: Nonlinear Solvers for a discussion of the
nonlinear solvers.
Global Vectors with locations for ghost values#
There are two minor drawbacks to the basic approach described above for unstructured grids:
the extra memory requirement for the local work vector,
localin, which duplicates the local values in the memory inglobalin, andthe extra time required to copy the local values from
localintoglobalin.
An alternative approach is to allocate global vectors with space preallocated for the ghost values.
or
VecCreateGhostWithArray(MPI_Comm comm,PetscInt n,PetscInt N,PetscInt nghost,PetscInt *ghosts,PetscScalar *array,Vec *vv)
Here n is the number of local vector entries, N is the number of
global entries (or NULL), and nghost is the number of ghost
entries. The array ghosts is of size nghost and contains the
global vector location for each local ghost location. Using
VecDuplicate() or VecDuplicateVecs() on a ghosted vector will
generate additional ghosted vectors.
In many ways, a ghosted vector behaves like any other MPI vector
created by VecCreateMPI(). The difference is that the ghosted vector
has an additional “local” representation that allows one to access the
ghost locations. This is done through the call to
VecGhostGetLocalForm(Vec g,Vec *l);
The vector l is a sequential representation of the parallel vector
g that shares the same array space (and hence numerical values); but
allows one to access the “ghost” values past “the end of the” array.
Note that one accesses the entries in l using the local numbering of
elements and ghosts, while they are accessed in g using the global
numbering.
A common usage of a ghosted vector is given by
VecGhostUpdateBegin(Vec globalin,InsertMode INSERT_VALUES, ScatterMode SCATTER_FORWARD);
VecGhostUpdateEnd(Vec globalin,InsertMode INSERT_VALUES, ScatterMode SCATTER_FORWARD);
VecGhostGetLocalForm(Vec globalin,Vec *localin);
VecGhostGetLocalForm(Vec globalout,Vec *localout);
... Do local calculations from localin to localout ...
VecGhostRestoreLocalForm(Vec globalin,Vec *localin);
VecGhostRestoreLocalForm(Vec globalout,Vec *localout);
VecGhostUpdateBegin(Vec globalout,InsertMode ADD_VALUES, ScatterMode SCATTER_REVERSE);
VecGhostUpdateEnd(Vec globalout,InsertMode ADD_VALUES, ScatterMode SCATTER_REVERSE);
The routines VecGhostUpdateBegin() and VecGhostUpdateEnd() are
equivalent to the routines VecScatterBegin() and VecScatterEnd()
above, except that since they are scattering into the ghost locations,
they do not need to copy the local vector values, which are already in
place. In addition, the user does not have to allocate the local work
vector since the ghosted vector already has allocated slots to contain
the ghost values.
The input arguments INSERT_VALUES and SCATTER_FORWARD cause the
ghost values to be correctly updated from the appropriate process. The
arguments ADD_VALUES and SCATTER_REVERSE update the “local”
portions of the vector from all the other processes’ ghost values. This
would be appropriate, for example, when performing a finite element
assembly of a load vector. One can also use MAX_VALUES or
MIN_VALUES with SCATTER_REVERSE.
DMPLEX does not yet support ghosted vectors sharing memory with the global representation.
This is a work in progress; if you are interested in this feature, please contact the PETSc community members.
Partitioning discusses the important topic of partitioning an unstructured grid.
Application Orderings#
When writing parallel PDE codes, there is extra complexity caused by
having multiple ways of indexing (numbering) and ordering objects such
as vertices and degrees of freedom. For example, a grid generator or
partitioner may renumber the nodes, requiring adjustment of the other
data structures that refer to these objects; see Figure
Natural Ordering and PETSc Ordering for a 2D Distributed Array (Four
Processes).
PETSc provides various tools to help manage the mapping amongst
the various numbering systems. The most basic is the AO
(application ordering), which enables mapping between different global
(cross-process) numbering schemes.
In many applications, it is desirable to work with one or more “orderings” (or numberings) of degrees of freedom, cells, nodes, etc. Doing so in a parallel environment is complicated by the fact that each process cannot keep complete lists of the mappings between different orderings. In addition, the orderings used in the PETSc linear algebra routines (often contiguous ranges) may not correspond to the “natural” orderings for the application.
PETSc provides certain utility routines that allow one to deal cleanly
and efficiently with the various orderings. To define a new application
ordering (called an AO in PETSc), one can call the routine
The arrays apordering and petscordering, respectively, contain a
list of integers in the application ordering and their corresponding
mapped values in the PETSc ordering. Each process can provide whatever
subset of the ordering it chooses, but multiple processes should never
contribute duplicate values. The argument n indicates the number of
local contributed values.
For example, consider a vector of length 5, where node 0 in the application ordering corresponds to node 3 in the PETSc ordering. In addition, nodes 1, 2, 3, and 4 of the application ordering correspond, respectively, to nodes 2, 1, 4, and 0 of the PETSc ordering. We can write this correspondence as
The user can create the PETSc AO mappings in several ways. For
example, if using two processes, one could call
AOCreateBasic(PETSC_COMM_WORLD,2,{0,3},{3,4},&ao);
on the first process and
AOCreateBasic(PETSC_COMM_WORLD,3,{1,2,4},{2,1,0},&ao);
on the other process.
Once the application ordering has been created, it can be used with either of the commands
AOPetscToApplication(AO ao,PetscInt n,PetscInt *indices);
AOApplicationToPetsc(AO ao,PetscInt n,PetscInt *indices);
Upon input, the n-dimensional array indices specifies the
indices to be mapped, while upon output, indices contains the mapped
values. Since we, in general, employ a parallel database for the AO
mappings, it is crucial that all processes that called
AOCreateBasic() also call these routines; these routines cannot be
called by just a subset of processes in the MPI communicator that was
used in the call to AOCreateBasic().
An alternative routine to create the application ordering, AO, is
AOCreateBasicIS(IS apordering,IS petscordering,AO *ao);
where index sets are used instead of integer arrays.
The mapping routines
AOPetscToApplicationIS(AO ao,IS indices);
AOApplicationToPetscIS(AO ao,IS indices);
will map index sets (IS objects) between orderings. Both the
AOXxxToYyy() and AOXxxToYyyIS() routines can be used regardless
of whether the AO was created with a AOCreateBasic() or
AOCreateBasicIS().
The AO context should be destroyed with AODestroy(AO *ao) and
viewed with AOView(AO ao,PetscViewer viewer).
Although we refer to the two orderings as “PETSc” and “application”
orderings, the user is free to use them both for application orderings
and to maintain relationships among a variety of orderings by employing
several AO contexts.
The AOxxToxx() routines allow negative entries in the input integer
array. These entries are not mapped; they remain unchanged. This
functionality enables, for example, mapping neighbor lists that use
negative numbers to indicate nonexistent neighbors due to boundary
conditions, etc.
Since the global ordering that PETSc uses to manage its parallel vectors
(and matrices) does not usually correspond to the “natural” ordering of
a two- or three-dimensional array, the DMDA structure provides an
application ordering AO (see Application Orderings) that maps
between the natural ordering on a rectangular grid and the ordering
PETSc uses to parallelize. This ordering context can be obtained with
the command
In Figure Natural Ordering and PETSc Ordering for a 2D Distributed Array (Four
Processes), we indicate the orderings for a
two-dimensional DMDA, divided among four processes.
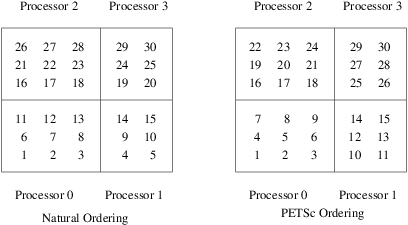
Fig. 4 Natural Ordering and PETSc Ordering for a 2D Distributed Array (Four Processes)#